Lessons Learned on Geeking Out On The Skill Map – Part 2
November 12, 2014
The Power of Non-Linear Thinking
As we discussed in part 1, the skill map identifies the constellation of skills a middle school math student should learn and how those skills relate to one another. The skill map is the foundation of Teach to One: Math, outlining the possible learning progressions a student might navigate through the program and providing the instructional glue to a coherent learning experience. While our current skill map reflects a vastly different approach than what was used in the early days of School of One—a precursor to Teach to One: Math, we drew valuable lessons from our early attempt to create a map of skills students would need to learn.
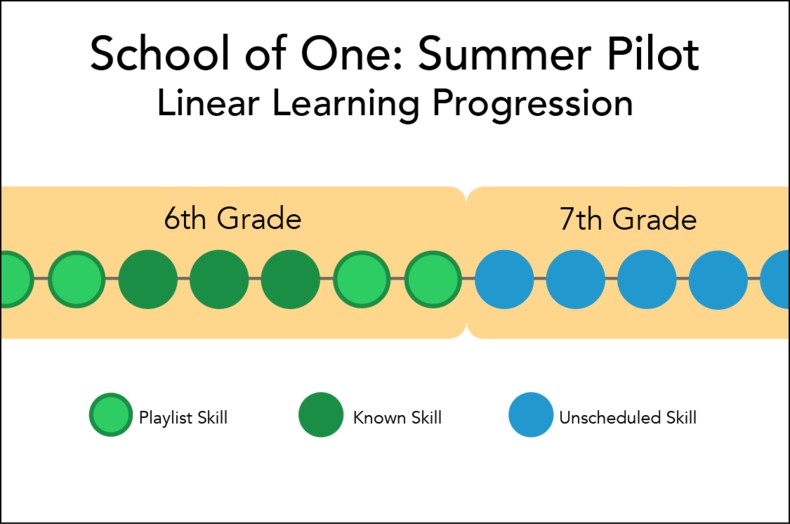
The precursor to the skill map, developed for the School of One pilot, was a standard scope and sequence. Skills were mapped horizontally, laid out by grade level. Over the course of the five week summer program, students progressed from one skill to the next.
Based on the promising outcomes of the pilot, at the end of the summer we were given the green light to continue School of One as an after-school program in three NYC middle schools in the spring of 2010. This would give our team an opportunity to leverage all of the lessons learned from the initial summer pilot and roll out a new and better version of School of One (albeit one still not ready to serve as the in-school math program).
In the six months before the after-school program would launch, we focused intensely on research and development to accelerate and deepen student learning. The first thing we addressed was the skill map, identifying two key challenges with the initial scope of sequence that had to be overcome:
1. Students’ varied paces meant that over time, students fanned out over an increasing number of skills. So if 25 kids all started on Skill #1, after a few weeks you might have 25 kids fanned out across 15 skills with no more than 4 or 5 on any single skill. It’s hard for teachers to most effectively support students that way, and unwise to rely that much on technology, which is the only way that kind of learning can practically happen given that variability.
2. Because the scope and sequence was linear, when students were stuck on one skill, there were not necessarily other places for them to go. In theory, they could either a) keep working on the same skill until they mastered it, or b) move onto a skill that they weren’t ready for.
We hypothesized that a non-linear skill map could help to address these two challenges. Once a student mastered one skill, an interconnected skill map would provide flexibility for which skills could be studied next. This would allow us to group students ready for common skills, enabling teachers to differentiate instruction effectively. Students who might be stuck on one skill would be able to slide over to another that didn’t necessarily require mastery of the first skill.
The map itself would be based on the New York State standards since participating students were based in New York and the Common Core standards were not yet available. We began by looking for as much research as we could find on skill maps. (There wasn’t as much as you might think.) We recruited some of the best math experts we could find while working within the NYC Department of Education. Day after day, our team debated the finer points of the skill map: Was X truly a precursor skill to learning Y? Should New York skill X be broken out into two different skills? What’s really the difference between the 6th grade standard Z and the 5th grade standard Z?
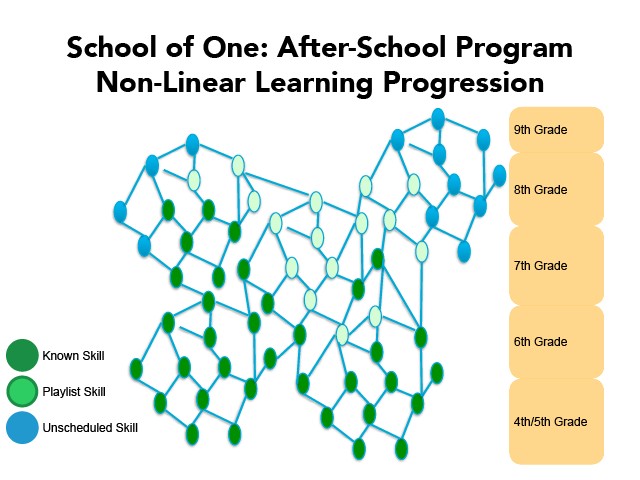
In the end, our initial non-linear skill map looked something like this.
When we rolled out the after-school programs and took the non-linear map for a test drive, we we found that the map did, in fact, solve some of the problems we had set out to address. The flexibility the skill map provided helped to keep kids from getting stuck on a particular skill. As we wrote new scheduling algorithms, we were able to begin clustering and re-clustering students with common needs, something that was much harder to do within the rigidity of a linear scope and sequence.
But while we did solve some of the challenges in this iteration, we hadn’t yet solved the valid critique that School of One was too “skills-based.” We hadn’t yet designed a way for students to develop a deeper level of conceptual understanding, apply their learning in real-world contexts, or explore the relationships among discrete skills—all elements critical to a comprehensive mathematics program. And the non-linear skill map created some new challenges that we hadn’t fully anticipated, though which seem fairly obvious with the benefit of hindsight, including:
- Instructional Coherence: The flip side of solving for instructional flexibility when it comes to skill selection is it can undermine instructional coherence. A standard textbook, while not at all differentiated, typically incorporates a coherent instructional path. Students learn how to add fractions, then subtract fractions, and so on, learning all about fractions as a theme. With our non-linear skill map, students might jump from subtracting fractions to determining the area of a parallelogram, which felt incongruous to teachers and students.
- Tested Grade-Level Content: The skill map covered skills in grades 5 through 8. An initial diagnostic assessment would help to determine where each student began and how they would eventually navigate through the map in ways that were agnostic to their assigned grade level. (This is the personalized in personalized learning.) The problem, however, was that this meant that the skills kids were learning were not necessarily grade-level skills, which they would be tested on at the end of the school year. If we were ever going to enhance School of One so that it could be applied during the regular school day, we would need to figure out a way to address the inherent tension between the competency-based model we were trying to create and the grade level-based evaluation systems that focus largely on grade-level content. This was our first wake up call to that problem.
By the end of the 2010 after-school programs, we recognized that while a non-linear skill map was essential, the one that we had was insufficient. We were scheduled to move to our first in-school program in the fall of 2010 in three schools, and we had a lot of work to do to be ready for the high-stakes world of core mathematics instruction.